Betting Theory: Bet Often

In our EV article, we had alluded to the law of large numbers as a major influence on how you should approach betting strategy. In this article, we’re going to really focus in on this. Hopefully, by the end, you’ll be convinced that ups and downs are inevitable, and your best defense against them is to place as many bets as you can!
A quick note: we’re going to try to avoid getting too semantic with statistical definitions, and are going to use some of these terms fairly loosely and colloquially. We’re mostly interested in targeting a conceptual understanding of these topics - anyone interested in very formal definitions is encouraged to read the following Wikipedia articles, as they’ll explain it much better than we ever could:
Variance
Variance, simply put, is a measure of how spread out a group of numbers is from their mean. Imagine you’re a marketing agency, trying to estimate age demographics to better target an advertisement. Your client just built the coolest toy car on the market, designed specifically to appeal to everything a 7-year-old would love! You can hang up posters at either the local playground, or directly inside of every 2nd-grade classroom at the elementary school (this is getting into some weird late-stage-capitalism territory, but for the sake of illustration let’s ignore that…). Your initial polling shows that the average age of kids in both of those settings just so happens to be exactly 7, but you can’t hang up posters in both places. Which would you rather target?
Without going into exact numbers, let’s just apply some intuition: the playground is going to have kids of all ages, let’s say ranging roughly from 4 to 10, while the classroom is going to be almost exclusively 6-, 7-, or 8-year-olds. Clearly, the ages of kids in the classroom are clustered much closer together, and on average are going to be closer to the mean of 7, so your posters will get much more bang for their buck there. This, in a nutshell, is variance! The playground has higher variance in ages, meaning that the ages of children at the playground are more spread out, while the classroom has a much narrower range of ages resulting in lower variance.
Formally speaking, when we colloquially talk about variance we really usually mean standard deviation. We can treat standard deviation as some sense of how far from the mean we expect different observations to be - so, if the standard deviation of kids’ ages on the playground is 2, we would expect most of the kids to be within 2 years of age of the mean of 7. “Most” is obviously fairly vague, but we’re intentionally being loose with the term to avoid having to deal with different types of distributions, population versus sample statistics, etc.
The law of large numbers
How does this apply to our betting strategy, though? When talking about EV, we spent a lot of time talking about what happens on average. Let’s say you think team A has a 70% chance of winning, and you bet on them. On any individual bet, you could win or you could lose, and you can’t really do anything in-between. If you could repeat the same bet 10 times, and play that same match out 10 times, you would expect to win some and lose some others, and you would expect to win your bet 7 times. Each bet is still a random probabilistic occurrence though, so you’re in no way guaranteed to win exactly 7 times. You might win only 5 times, or 8 times, or really any other number between 0 and 10 with varying probabilities. What if you could place that bet 100 times? You’d expect to win 70 bets on average, but again could easily hit another number.
What do you think is more likely, given your 70% odds? Winning only 5 of 10 bets, or winning 50 of 100? As it turns out, winning 5 (or fewer) out of 10 bets has a 15% chance of occurring, while winning 50 (or fewer) out of 100 has only a 0.002206092% chance!
This is actually an incredibly important result. First though, it’s worth taking a step back and asking ourselves why this is a fair comparison. After all, winning 5 of 10 bets is only 2 fewer than we would expect, while winning 50 of 100 is 20 fewer! However, in this hypothetical example we would also be splitting our money into more pieces (let’s say $10/game on 10 games, or $1/game on 100 games), so these two numbers would both correspond to winning with $50 worth of our bets. Another way to look at it: both of these correspond to winning 50% of our bets, which is important because what we really care about is the relative rate of our successes.
Here’s a quick way to visualize this: below, we plot the probability of winning each possible number of bets in our two scenarios (repeating the same bet 10 times, or 100 times). This is effectively just a plot of the distribution of outcomes; in this case, specifically a binomial distribution.
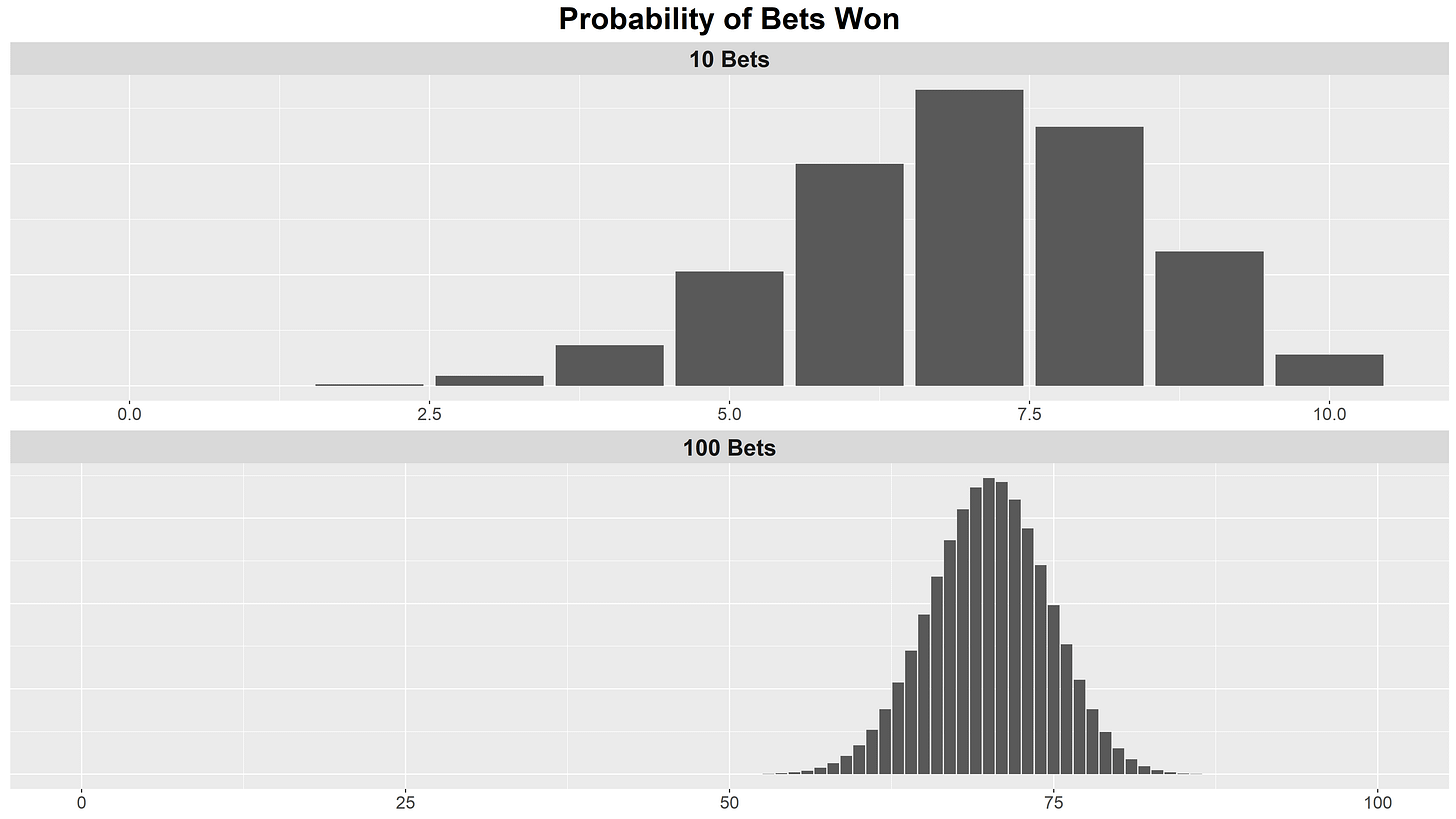
Now, we can take both of these distributions and normalize them - we’ll simply ask “what is the probability of winning this percentage of our bets?”
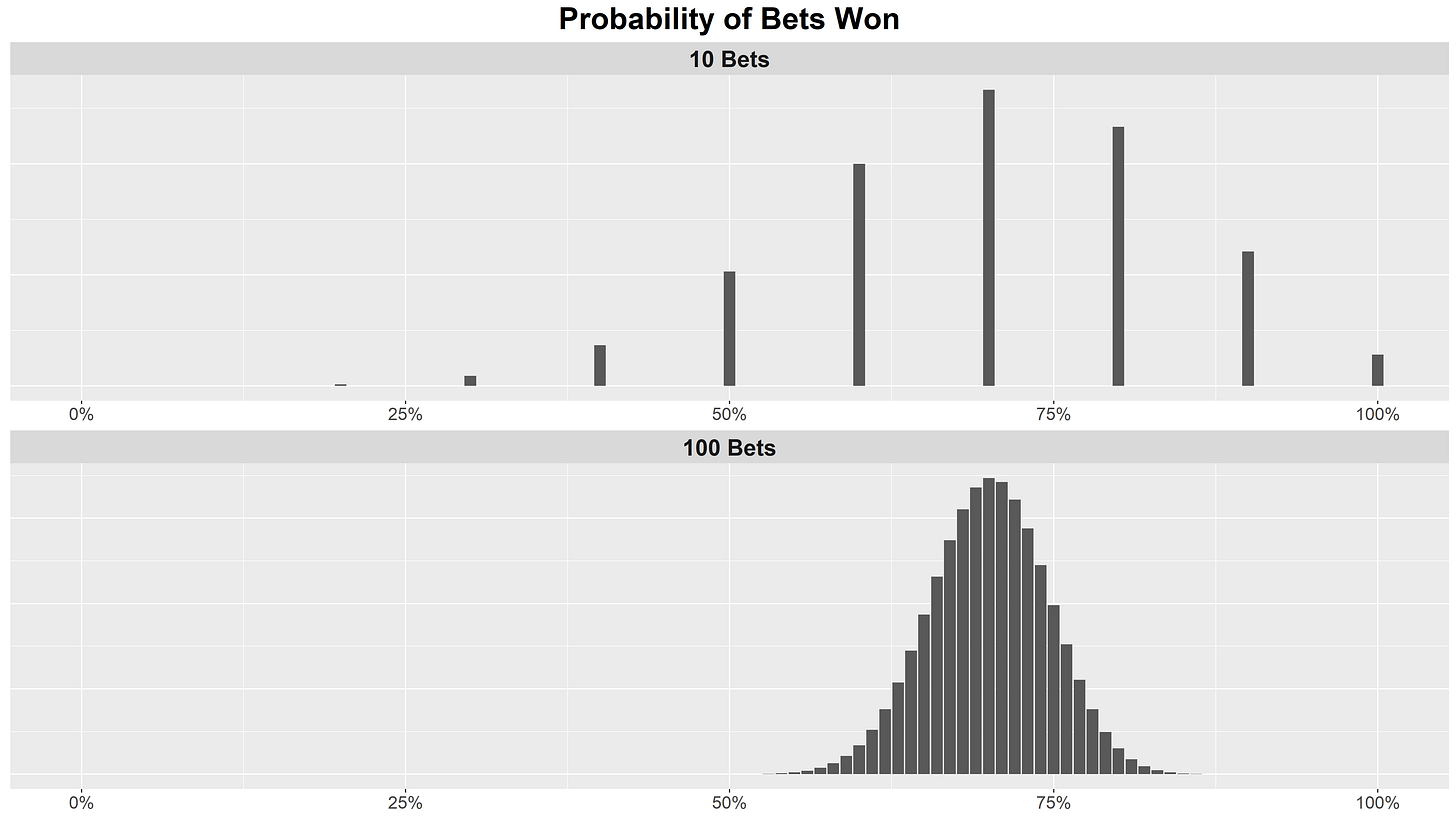
This is effectively the same exact plot, we’ve simply relabeled the x-axis. However, it allows us to do an apples-to-apples comparison of the two scenarios. For both, your highest probability is winning exactly 70% of your bets, with probabilities dropping off in either direction. What’s important to note is that, qualitatively, there is much more “spread” in the case of only 10 bets. It’s not impossible to win only 20% of your bets, whereas in the case of 100 bets your probability drops more or less to zero around 53% of bets won.
This is really what the law of large numbers is talking about - the more trials of the same experiment you perform, the less deviation there will be from your expectation.
Some mathematical formality
As mentioned earlier, we’ve been colloquially using terms like “spread” or “variance” when we really mean standard deviation. To slip into some formality: variance is linear with the number of trials, which means that the variance of 100 trials should be ten times greater than the variance of 10 trials. Indeed, in our example the variance of 10 games is 2.1, while the variance of 100 games is 21. Standard deviation, however, is the square root of variance, which gives us standard deviations of 1.449 and 4.583 respectively.
Standard deviation, again, is some sense of how far observations are from the mean. In this example, this means that out of 10 games we’re pretty likely to see any number of wins within ~1.5 of our expectation of 7, while out of 100 games we’re pretty likely to see any number of wins within ~4.6 of our expectation of 70.
The standard deviation for our 100-game scenario is still higher, but what we really care about is the standard deviation relative to the number of bets. As illustrated in our example, as we place more bets we are splitting our money across them, so we care much more about the percentage of our bets that we win than the total number of bets we win.
Thus, (StDev/N_bets) is a normalized way to look at our distribution that basically tells us how close in percentage terms we’re likely to be to our expectation - a standard deviation of 4.6 out of 100 bets means that we expect to be within ~4.6% of our expectation, which is much closer than 2.1 out of 10 bets, which is 21%.
As we’d mentioned, variance is linear with number of bets, while standard deviation is equal to the square root of variance. This means that as the number of bets increases, standard deviation increases at a slower rate, so our relative spread (StDev/N) grows as (sqrt(N)/N) = 1/sqrt(N). In short, the more bets we place, the closer our outcome will be to our expectation on a relative basis.
Back to betting
In reality, of course, you can’t play out the same exact bet 100 times. You’re welcome to place 100 separate, smaller bets on the same match, but that match is still only going to get played out once, so from the perspective of statistics it’s just a single event (and you can just add up all of your bets and treat it as one larger bet). The best we can do, then, is to simply bet on as many matches as we can! As we’ve hopefully convinced you by now, the more shots you take, the closer you’ll be to your overall expectation. Keep in mind: with repeated, independent events, expected value is additive, which just means that the expected value of all of your separate bets is equal to the sum of each individual bet’s expected value. This just means that, same as in our simpler examples, the more bets you place, the more likely you are to hit your expectations!
In our Spring 2021 performance recap, we had presented the following plot, showing our performance in each individual league:
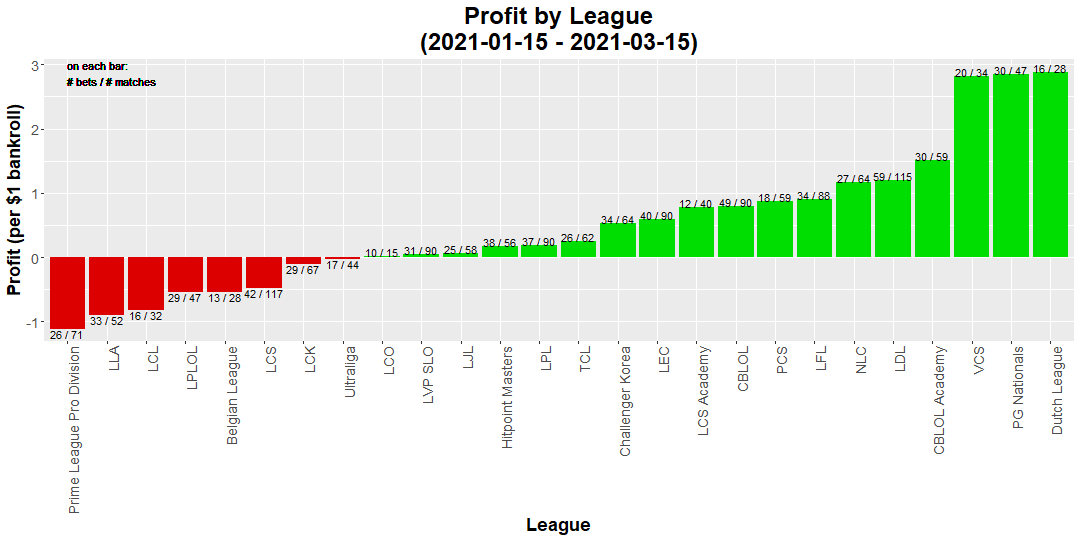
In any individual league, there could be quite some spread in results - some lost money, some made a little bit of money, and some made a lot of money. Obviously you’d love to only have bet on the winning leagues, but short of a crystal ball or a deal with the devil, that’s just not possible. However, by simply betting on all of them, we made it much more likely to be close to our overall expected value, and ended up profitable.
By reducing our relative variance, betting on more games also, by definition, smooths out our returns. This is an important metric in finance; interested readers should check out some basics on the Sharpe Ratio. This leads to more consistent returns, so as long as you still believe in your underlying model, you’ll experience fewer crazy up-and-down swings in money, as well as fewer prolonged drawdown periods.
The gambler’s fallacy
There is a caveat here, unfortunately: you might take this to mean that if you went through a losing streak, placing more bets should help bring you back up to your overall expectation. This is known as the gambler’s fallacy: losing a bunch of bets in the past does not increase the chances of winning future bets, because all of these bets are statistically independent - that is, their outcomes do not depend on each other. The law of large numbers applies only to the deviation of future expectations; once an event has actually occurred, its expectation no longer matters, because we’ve already seen what happens. Your overall expectation, therefore, becomes the sum of your actual realized bets, and the expected value of future bets.
As a corollary: if you’re at a casino, never double down because you feel like you’re “due for some good luck”. Casinos love this - players take increasingly risky bets and put more money in, but the forward expectation of each bet hasn’t actually changed (and, of course, the house is always favored), so they get to just reap in bigger rewards. This is also exactly why casinos are more than happy to provide free accommodations to any high rollers who claim to have a winning betting strategy. In a casino, changing the size of your bets based on what’s happened never actually affects the future expectations, and these bettors are likely to keep throwing around vast sums of money to try to prove themselves right. One of the more famous such approaches is called a martingale, which involves doubling your bet every time you lose to make sure you always recover whatever you’ve lost so far, and is worth a quick read if you’re interested such things.
It seems like we’re convincing you that no amount of fancy betting strategy can help you beat the house, so why should you trust our bets on League of Legends matches? The fundamental difference is that while future outcomes do not depend on past bets, that is not what we’re betting on. We’re betting because we do not agree with the market’s view of expected value! In casinos, the games are truly random and therefore follow purely probabilistic outcomes and are solved - nobody disagrees on the expected value of a spin at the roulette table, for example. In our case, there are many factors, known and unknown, that go into each game, and each game ultimately relies on the performance of ten individual players, so there is no purely statistical way to calculate outcomes and therefore there is room for divergent opinions on the expected value of the game. And once you believe there is EV to be had, there are ways to structure your bets to make the most of it (we’ll be writing an article on bet sizing soon!).
Hopefully, we’ve convinced you that placing more bets is going to yield more consistent, and thus safer, results. Just like maintaining a diversified stock portfolio, this is the difference between trying to find value and simply gambling. So far, we’ve limited our posts to LCS and LEC match predictions as a sample of what our model has to offer, but we’ll be unveiling a way for you to access all of our predictions on every professional match in the very near future! Make sure you’re subscribed here and follow us on twitter, to keep up with all of our developments and predictions and stay ahead of the game!

