Betting Theory: Bet EV, not the Favorite

If you’ve followed along with our betting suggestions, you’ve probably noticed that we’re more likely to bet on the underdog than the favorite. This seems counterintuitive - aren’t we likely to lose more bets than we win if we do that?

The answer is yes, we expect to lose more bets than we win, but we still expect to win more money than we lose. If our wins return a lot more money than our losses lose us, we should come out ahead. We just need the proper framework to evaluate this…

In this first installment of our Betting Theory series, we’re going to cover the concept of expected value (EV) and how it applies to odds markets and our own predictions.

Don’t always bet the favorite

Betting the favorite seems like the safer play - after all, you’re more likely to win, so it’s free money, right?

Well, that depends on the specifics of the bet, and the odds that you’re getting on that bet. Often, when people make quick bets with a friend, it’s implied that you’re getting even odds - that is, whatever the bet amount is, if you win the bet you get that much money and if you lose the bet you lose that much money.

For example, if someone says “hey, I bet you $5 that Logan Paul could beat Floyd Mayweather in a boxing match,” you’d obviously take that bet! There’s pretty much no chance of this happening, so you’re incredibly likely to just win $5. What if your friend had said “hey, I bet you $5 at 1-to-10 that Logan Paul could beat Floyd Mayweather”? In this scenario, you’re putting up $50 to your friend’s $5, so even though Mayweather is still incredibly likely to win, you stand to lose a lot more if things go sideways.

Or, to take this concept to the extreme - what if your friend offered you one-to-a-million odds? It’s still almost impossible for you to lose the bet, but it’s not actually impossible. If you’re wrong, you’re basically bankrupt for life (and if you’re not, message me, I’ve got some business ideas!), and if you’re right you’ve only won $5. Seems like a terrible idea. Obviously this is a somewhat unrealistic bet, but pushing things to extremes is a good way to disprove common generalizations.

As of this writing, odds for this match are pretty much all over the place given the uncertain nature of such a lopsided matchup, ranging anywhere from -3500 (1-to-35) to -5000 (1-to-50).

Underdog bets have potentially huge returns

The flip side of this, of course, is betting on the underdog. In the same scenario as above, if someone is willing to bet you that Mayweather wins at a-million-to-one odds, you would almost certainly take it! Worst case you’re out $5, but there’s a chance that you’re set for life.

Extreme cases like this are sort of like buying a lottery ticket, and most of us have probably heard the phrase that “lotteries are a tax on the poor” - your average ticket buyer loses money, so the lotto system as a whole is profitable and effectively just takes money out of the predominantly lower socio-economic-class entrants (fortunately, state-run lottos typically reinvest it in infrastructure anyway).

This quick generalization ignores the marginal utility of money, which I won’t go into much detail here but is an interesting topic to read more about if you’re interested in some basic principles of socioeconomic decision-making. The short version of it is that even though you’re losing money on average, it might still be worth buying a lottery ticket because paying for the ticket on a regular basis doesn’t really affect your quality of life, but if you do win it would substantially change your circumstances.

Unlike lotteries, which are designed to be profitable for the state, there is no fundamental reason why betting on an underdog should lose money on average any more so than betting on the favorite. In fact, treating the 50% point as some important divider is fairly arbitrary, and each potential bet can just be treated in isolation.

Finding the line

Most bets aren’t quite as lopsided as our boxing match, so things like utility of money or massive uncertainty of outcomes aren’t going to be relevant.

In addition, unfortunately, markets are generally reasonably efficient, and should rarely give you obvious choices. The lines they give will typically be at a point where either option seems attractive, and this is by design! Oddsmakers are generally trying to balance their books, which means that they get a roughly equal amount of bets placed on either side of an event, to limit the oddsmaker’s own exposure to the outcome. If too many people are betting on one outcome, they simply shift the line (their offered odds) such that the other side of the bet looks more attractive, and balance things out.

Here’s a relatively quick way to prove this: we can imagine a simple betting strategy in which we always bet on the underdog (according to the market), or always on the favorite. If the oddsmaker is doing their job, these two should be equally (un-)profitable. Here’s a PnL (profit-and-loss) plot of this strategy, if we always bet 10% of our base bankroll on every single game over the past two months:

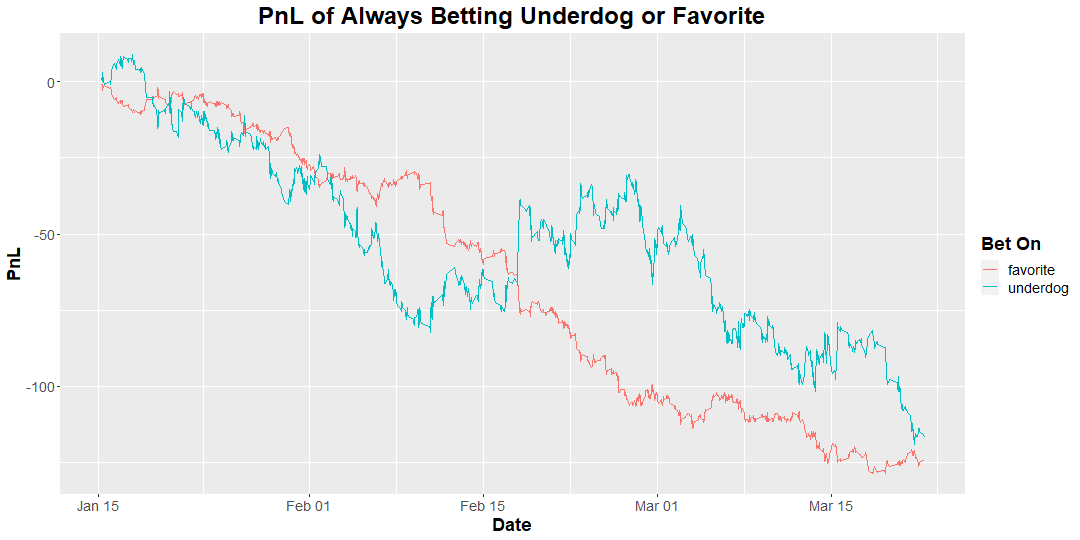
The profit of always betting on the favorite is fairly close to always betting on the underdog, but there are a few important points to make:

1. In any time period, the two can diverge quite a bit - this is simply variance.
2. Both lose a lot of money. This is due to something called the vig - effectively a tax or rake the oddsmaker collects on each bet. We’ll go into much more depth on this in a future article, but for now just keep in mind that this is why being an oddsmaker is profitable - blind gambling will steadily just bleed money to them.
3. The underdog line is much more volatile - volatility is basically a measure of how “noisy” the PnL is. Slow and steady returns will have lower volatility, so it can be treated as a measure of consistency. This intuitively makes sense: if we’re betting on the favorite, we would expect to win more of our bets, but make less money on each bet, which should give us a smoother return profile. If we break down the bets:

|   Bet On |  % Won | Avg Gain | Avg Loss |
|----------|--------|----------|----------|
| favorite | 66.63% |   0.3824 |       -1 |
| underdog |    29% |   1.9427 |       -1 |

If you always bet on the favorite, you would win ~67% of your bets, but each win would net you only a 38% return on your bet size, on average. Betting on the underdog, conversely, you would only win 29% of your bets, but each win would be worth substantially more, returning 194% of your bet size on average.

To navigate this, we need to establish a quantitative framework to identify which side of a bet looks better, without falling into the traps of defaulting to the favorite or hoping for a lottery win.

Calculate your own probabilities

First things first, you need to have your own view of how likely an event is to occur. Too often, people will look at the market, say “oh, those odds seem reasonable”, and bet. This is very dangerous - first of all, as already mentioned, markets are designed to make both sides look reasonable, but clearly the oddsmakers are profitable. Second, by doing this you’ve effectively imprinted an estimate of the event’s probability in your mind, and are likely to accept it as correct just because clearly the market thinks so too.

Ideally, you should have your own independent sense of the probability of an event. The more quantitative your approach the better - this allows you to be unbiased, unemotional, and avoid some common decision-making traps.

Let’s say we’re betting on a soccer match, and we think team A has a 40% chance of winning and team B has a 60% chance of winning. Again, the instinct is to bet team B, but this depends on how much money you’d get paid out in either scenario, which brings us to…

Expected Value (EV)

In discussing the lottery system, a few times I mentioned what happens to the average entrant. Some people win money, most people lose money, but on average when you buy a ticket you lose money. This is precisely expected value - the average return of an outcome.

In our soccer match, let’s say that the market is offering +200 on team A and -200 on team B. We can quickly tabulate what happens if either team wins, depending on which team we bet on:

| bet on | team A win | team B win |
|--------|------------|------------|
| team A |      +$200 |      -$100 |
| team B |      -$100 |       +$50 |

Since we have our calculated probabilities from above, we can now put it together with this and figure out the expected value of each potential bet. Formally, expected value is the sum of the value of each outcome times the probability of that outcome. If we’re betting on team A:

EV(team A) = (payout if team A wins)*(probability team A wins) + 
             (payout if team A loses)*(probability team A loses)

EV(team A) = (200)*(40%) + (-100)*(60%)

EV(team A) = $20

This means that if we were to bet on team A, on average we would win $20 off of our $100 bet! Another way to look at this: in any single instance, team A could win or lose. If we could play this match out 100 times and bet $1 on each match, team A would win 40 times and earn us $80, and would lose 60 times and lose us $60, for a net profit of $20.

Now let’s check that betting on team B is a bad idea:

EV(team B) = (payout if team B wins)*(probability team B wins) + 
             (payout if team B loses)*(probability team B loses)

EV(team B) = (50)*(60%) + (-100)*(40%)

EV(team B) = -$10

Betting on team B loses you $10 on average, so it’s not worth betting on.

If you ever find that both teams have positive EV, either something is wrong with your math, or the market has VERY misaligned odds and you can just trade both sides to guarantee a profit. It’s quite possible, however, for both teams to have negative EV - this is because of the aforementioned vig. We’ve ignored that for this example, as our focus in this article is to explain the approach of EV betting, but look out for a future article that goes into more detail on this!

If both sides have negative EV, simply don’t bet. Otherwise, bet on whichever side has positive EV. On any individual bet you might still lose money, but if you keep following this rule and place lots of bets on lots of games, on average you should be making money. The more bets you place, the closer to these averages your returns should be. We’ll explore this in a future article as well, but curious readers can look up the law of large numbers for more info.

We’ll be writing a whole series of articles on betting theory, to make sure our readers have a solid fundamental understanding of how odds markets work and why we structure our bets the way that we do. Make sure you’re subscribed here and follow us on twitter, to keep up with all of our developments and predictions and stay ahead of the game!