Betting Theory: Vig and Implied Probabilities

In our Expected Value article, we had alluded to the vig that an oddsmaker takes, but had ignored it for illustrative purposes. It does, however, have some serious implications for any betting strategy, and represents an “edge” hurdle that we have to overcome. In this article, we’re going to go over exactly how it’s defined, how it affects our betting ability and strategy, and its impact on match probabilities implied by the market.
The vig
The vigorish, which you may have seen called the juice or cut, and hereon we’ll simply call the vig, is functionally a rake that oddsmakers take on any bet. Normally, if an event has even odds (50/50) of occurring, you should expect an even payout. With a vig, the “house” basically says that they’ll pay you less than what they really should in a “fair” bet, given the odds of the outcome occurring.
Let’s start with an incredibly simple illustrative example: Alice and Bob are betting on a coinflip. Alice bets $1 on heads, and Bob bets $1 on tails.
If they are just betting against each other, they can probably agree that a coin has 50/50 odds of either outcome, and therefore the winner simply takes the $1 that the loser bet. Whatever the outcome, one of them loses $1 and the other wins $1, so it’s a zero-sum game.
However, what if Alice and Bob don’t know each other, and can’t find anyone to directly bet on this coinflip with? Well, they go to a bookmaker. The bookmaker will give them odds such as -110/-110. This means that Alice would need to bet $110 in order to win $100, or conversely, if she bets $1 and is correct, she will win only 91 cents. This bet happens to be symmetrical, so Bob is in the same boat. Whatever the outcome of the coinflip, the loser will lose $1, the winner will win 91 cents, and the oddsmaker will keep the 9 cent difference.
The vig is this remainder, typically quoted as a percentage: for every two dollars bet in total ($1 from Alice and $1 from Bob), the house keeps 9 cents, which is 4.5%.
Implied probabilities
Since odds provided by a market are really just payoffs, and less likely events should pay out more, we should be able to back out from market odds what the probability of an event occurring is. Any line set by an oddsmaker, such as -110, implies a certain probability of the event occurring. If there is no vig, then an efficient oddsmaker should be setting lines such that their expected value is 0 based on what they believe the probability of an event happening is; otherwise people will just bet on the EV-positive side and the oddsmaker will lose money.
This probability is easier to calculate in decimal odds:
-110 (american) = 1.91 (decimal)
EV = (payout on win)*(probability win) + (payout if lose)*(probability lose)
we'll call the probability of winning w, and therefore probability of losing is 1-w
EV = (1.91-1)*(w) + (-1)*(1-w)
EV = 1.91*w - 1
setting to 0:
0 = 1.91*w - 1
w = 1/1.91
w = 0.5236Thus, the breakeven point of a -110 line is at 52.36%: if an event has a 52.36% chance of occurring, then an oddsmaker has to pay out at -110 / 1.91 to not lose any money, on average. It’s also worth noting for future reference: given decimal market odds (i.e. 1.91 in the above example), the implied probability of an event is simply the reciprocal of its odds.
But wait! In our example above, the oddsmaker had set both sides of the event at -110. It’s not possible for both events to have above a 50% chance of occurring, is it? And again, this is where the vig comes in. The total odds from both sides are ~104.72%. What does this mean? It means that the oddsmaker is giving payouts as if each side was more likely to happen than it actually is (and thus paying out less money than is fair), and keeping the difference. For every $104.72 placed in bets, only $100 is being paid out. 100/104.72 is 95.5%, so the oddsmaker is keeping 4.5% of all the bets - the same vig that we calculated above!
This is where we should be careful with our terminology: when we talk about probabilities implied by odds, we’re talking about the probability of an occurrence if the odds are fair! An oddsmaker doesn’t really have much incentive to be fair - they’re running a business after all, and need to be profitable. There’s a silver lining, though: nobody can truly know the odds of an event happening (outside of trivial things like coinflips, which don’t have too much of a betting market last time we checked), so oddsmakers set lines based on what they believe the probabilities to be, and tack on a vig. Here’s where we can find an edge: if our model more accurately predicts probabilities than the oddsmaker does, we’re willing to make slightly unfair trades because we still believe we can make money!
Slow and steady drain
On a single bet, the vig functions as a way for oddsmakers to position themselves such that they make money no matter what the outcome of an event is, if they can get enough bettors on each side. For a repeated betting strategy, which is exactly what we’re trying to create, it functions similar to a transaction cost that a broker might charge you for buying stocks - if you’re buying and selling a bunch of stocks constantly (for example, you’re a day trader), then you have to make sure each trade is profitable enough to overcome the cost of putting that trade on. If your trades, on average, are flat (don’t make or lose money), then you’ll slowly just bleed out transaction fees for no benefit.
In our EV article, we had shown the following plot, showing the profit-and-loss (PnL) of a strategy where we always bet on the favorite, or always on the underdog, across roughly 1900 league of legends matches:
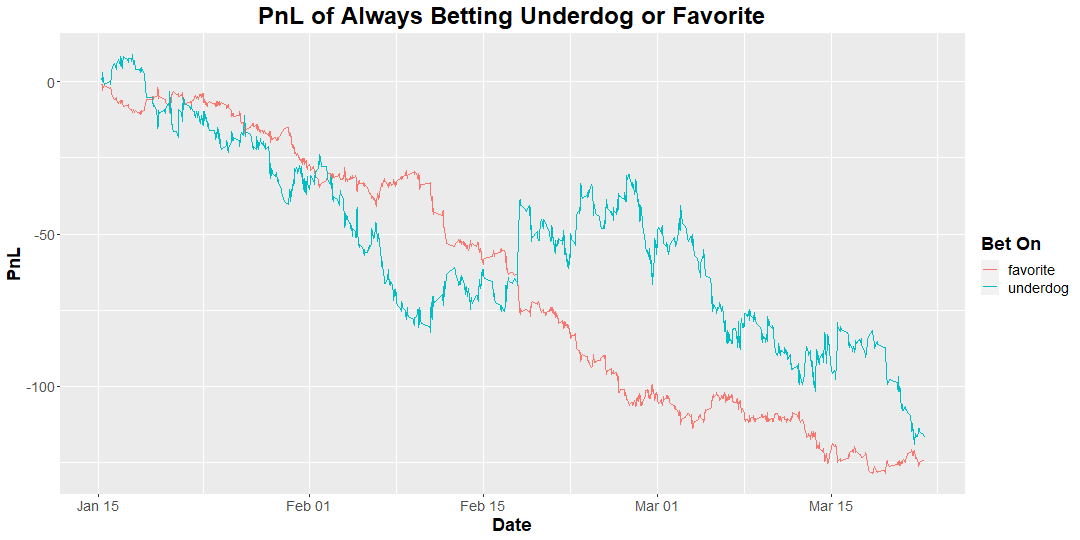
As we had mentioned, both of these lose a lot of money due to the vig. You would have won ~67% of your bets on the favorites, but they didn’t pay out accordingly to the risk. If payouts were fair (that is, pay out exactly according to their probabilities), we should expect both of these lines to be roughly flat. Favorites would win more often but pay out less money, underdogs would win less often but pay out more money, and on average the expected value of a fair bet is 0 so you shouldn’t really be making any money. Here’s the same plot, but with the vig removed:
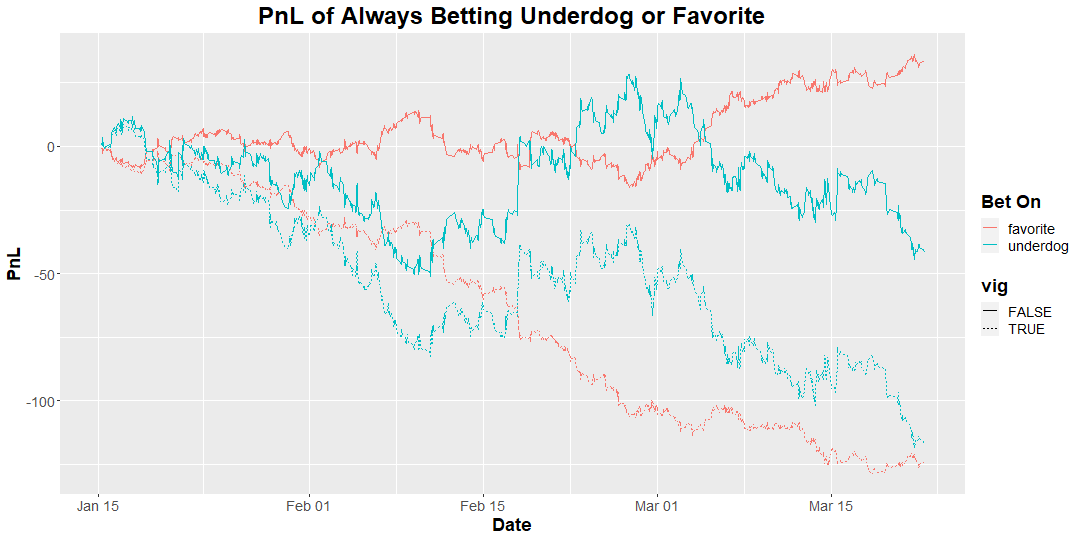
That is a light and day difference! Just getting paid out a little bit more on each bet is enough to flatten these lines:
| Bet On | % Won | Avg Gain | Avg Gain (w/o vig) | Avg Loss |
|----------|--------|----------|--------------------|----------|
| favorite | 66.63% | 0.3824 | 0.4486 | -1 |
| underdog | 29% | 1.9427 | 2.015 | -1 |Keep in mind that we’re winning the same number of bets, the only difference is that we’re not losing ~6% of each payout to the vig.
Attentive readers may remember from our EV article that over the long run, we should expect the favorite and underdog PnL to be roughly the same, and yet there’s definitely some divergence here near the end. There are two possible explanations:
- variance - sometimes, you just have stretches of time where favorites win more often than anyone expects. With more games this effect should diminish.
- mispricing - the market may just be incorrectly setting its lines, by which we really mean that oddsmakers’ predictions aren’t correct. Obviously we expect them to not always be right, as we wouldn’t have any edge to find otherwise, but on average they should be pretty accurate and lately it seems like a pretty systematic divergence.
We’re planning on doing a deep dive on market dynamics in a future article, so if you’re interested in the nuance of oddsmaker incentives as well as a retrospective look at market efficiency, keep your eyes peeled!
Un-Favoritism
If we approach the vig from the other side, we'll actually see that the vig disproportionately removes profit from the favorite of a match! Let's walk through an extreme example:
An oddsmaker believes that team A has a 90% chance to win its match against team B. They adjust this 90/10 probability to incorporate their 6% vig, so really they're just multiplying each side by 1.0638 (1/0.94), to get "probabilities" of 95.74%/10.64%. They convert this to odds, giving us 1.0444/9.40. (note: all of this is basically the inverse of the Implied Probabilities section)
The "fair" payouts (i.e. with no vig) would have been 1.1111/10.0. So, what exactly has the vig done? Assuming you bet on the correct winning team: if team A wins, you will receive $104.44 on a bet of $100, instead of $111.11. If team B wins, you'll receive $940.00 instead of $1000.00. In each case, you're receiving exactly 6% less than you should (94%) - which is exactly what you should expect, since the vig was 6%. So far, this seems symmetrical - your payouts are haircut by the same proportion, whether you bet on the favorite or the underdog.
Except for one glaring problem: these haircuts are on your payouts, not your profits. When you place your $100 bet and then get paid $104.44 back, this includes your initial bet. Your profit, then, is only $4.44 if team A wins, and $840.00 if team B wins. If the payouts were fair, your profit would be $11.11 and $900.00 respectively. So, while your payout is always 94% of what the fair payout would be, due to the vig, your profit actually varies quite a bit: if team A wins, your profit is only 40% of what it should be ($4.44 / $11.11), while if team B wins, your profit is 93.33% of what it should be ($843 / $900)!
Here's a table of how much of the fair profit you're getting, depending on how much of a favorite the team you're betting on is:
| Win% | (w/vig) | Payout | (w/vig) | Profit | (w/vig) | % Profit |
|------|---------|--------|---------|--------|---------|----------|
| 10% | 10.64% | 10.0 | 9.40 | 9.00 | 8.40 | 93.33% |
| 15% | 15.96% | 6.67 | 6.27 | 5.67 | 5.27 | 92.94% |
| 20% | 21.28% | 5.00 | 4.70 | 4.00 | 3.70 | 92.5% |
| 25% | 26.60% | 4.00 | 3.76 | 3.00 | 2.76 | 92% |
| 30% | 31.91% | 3.33 | 3.13 | 2.33 | 2.13 | 91.43% |
| 35% | 37.23% | 2.86 | 2.69 | 1.86 | 1.69 | 90.77% |
| 40% | 42.55% | 2.50 | 2.35 | 1.50 | 1.35 | 90% |
| 45% | 47.87% | 2.22 | 2.09 | 1.22 | 1.09 | 89.09% |
| 50% | 53.19% | 2.00 | 1.88 | 1.00 | 0.88 | 88% |
| 55% | 58.51% | 1.82 | 1.71 | 0.82 | 0.71 | 86.67% |
| 60% | 63.83% | 1.67 | 1.57 | 0.67 | 0.57 | 85% |
| 65% | 69.15% | 1.54 | 1.45 | 0.54 | 0.45 | 82.86% |
| 70% | 74.47% | 1.43 | 1.34 | 0.43 | 0.34 | 80% |
| 75% | 79.79% | 1.33 | 1.25 | 0.33 | 0.25 | 76% |
| 80% | 85.11% | 1.25 | 1.18 | 0.25 | 0.18 | 70% |
| 85% | 90.43% | 1.18 | 1.11 | 0.18 | 0.11 | 60% |
| 90% | 95.74% | 1.11 | 1.04 | 0.11 | 0.04 | 40% |In short - when betting on heavy favorites, even if you believe the market's assessment of each team's odds, the vig will substantially reduce your profits, much more so than if you bet on large underdogs.
Beating the vig
Unfortunately, we can’t just remove the vig, as we have to go through oddsmakers to place our bets. How do we beat it, then?
Let’s work with a slightly more complicated, and more realistic scenario. We want to bet on the same soccer match that we discussed in our EV article, for which we have calculated the odds of winning to be 40% for team A and 60% for team B. We go to our favorite bookie, and they give us this line: +183/-241.
First, what does this imply about the market’s estimate of the game? If we convert these to percentages as above, we get: 35.33%, 70.67%. Again, we see that these add up to more than 100%; 106% to be exact. We know this is the effect of the vig, but if we treat the market as the aggregate view of all bettors, we want to be able to know the “true” probabilities of each team winning. We can simply normalize these numbers by dividing by the total, to make sure they add up to 100%:
team A win% = 35.33%/106% = 33.33%
team B win% = 70.67%/106% = 66.67%So, the market believes team B has twice the chance of winning as team A does.
Our own calculations disagree with these, so how do we take advantage of this? We think team A has a higher chance of winning (40%) than the market does (33%), so we should bet on them!
We have to be careful, however: while the market thinks team A has a 33.33% chance of winning, it is only paying out the bet as if team A had a 35.33% chance of winning. We can verify this by calculating the EV of a $100 bet on team A, same as before:
EV(team A) = (payout if team A wins)*(probability team A wins) +
(payout if team A loses)*(probability team A loses)
EV(team A) = (183)*(40%) + (-100)*(60%)
EV(team A) = $13.20Our EV for team A was previously $20. It’s still profitable to bet on team A, but less so, as we’ve essentially just reduced our upside if we’re right.
This is how the vig manifests itself in our betting strategy - we have to have a different view of event probabilities than the market does, and it has to be different enough to overcome the vig.
The vig beating us
What if we thought that this matchup was actually 35/65? Well, let’s calculate the EV for betting on each team:
EV(team A) = (183)*(35%) + (-100)*(65%)
EV(team A) = -$0.95EV(team B) = (41.49)*(65%) + (-100)*(35%)
EV(team B) = -$8.03Turns out the EV is negative on both teams! While our estimate for team A’s win probability (35%) is higher than the overall market’s true sentiment of that probability (33.33%), it’s actually lower than the payout would imply (35.33%). As we’ve defined, the implied probability of market odds is simply the probability at which the bet has an EV of 0.
In this situation, we should bet on neither team, and just accept that the market’s line is very close to our predictions, and therefore the vig washes out our edge.
An interesting corollary emerges: the EV of a trade is positive if and only if our calculated probability is greater than the market-implied probability of an event:
given:
decimal market odds p; p>1
our calculated win% w
we have:
profit on win = p-1
profit on loss = -1
ev = w*(p-1) + (1-w)*(-1)
ev = wp - w + (-1) + w
ev = wp - 1
for ev to be positive:
wp - 1 > 0
wp > 1
w > 1/pRecall that given decimal market odds, the implied probability of that event occurring is exactly 1/p. So, our EV is positive exactly when our calculated odds are higher than the market-implied odds!
So do I just start betting now?
At this point, you should be convinced that you should bet based on EV, and that your EV is positive only if you have a more bullish view than the market (and different enough to overcome the vig).
Before you actually put money down, two fairly obvious questions should come up:
First, what if our prediction is wrong? We had decided to bet on team A because we thought they had a 40% chance to win, while the market had it at 33%. What if the market was simply more correct? (spoiler: you tend to lose money if your predictions are wrong).
Second, shouldn’t we care about what the EV actually is, rather than just whether or not it’s positive? Since we don’t have an infinite pool of money, doesn’t it make sense to place bigger bets on games where we stand to win more? (spoiler: yes).
Both of these have simple short answers, but there is quite a bit of nuance in optimizing your betting strategy to take care of these issues. Keep an eye out for future articles covering exactly those questions!
We’re writing a whole series of articles on betting theory, to make sure our readers have a solid fundamental understanding of how odds markets work and why we structure our bets the way that we do. Make sure you’re subscribed here and follow us on twitter, to keep up with all of our developments and predictions and stay ahead of the game!

